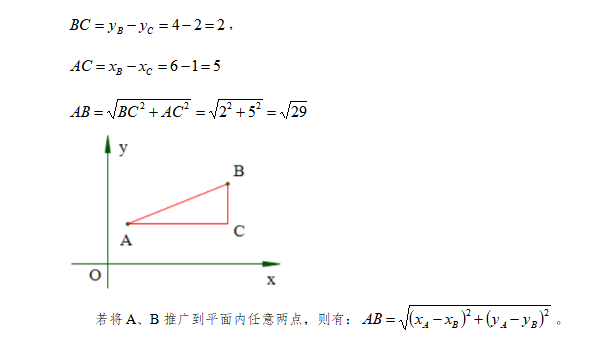
Ę×í(y¨¨)
ëSr(sh¨Ş)(w¨¨n)
ëSr(sh¨Ş)˝â´đ
óżź
äżź
¸ßÖĐ
î}ě
ÖŞ×Rüc(di¨Łn)
ŐZ(y¨ł)ÎÄ
ľW(xu¨Ś)
Ó˘ŐZ(y¨ł)
ÎďŔí
ťŻW(xu¨Ś)
łőŇť
łőśţ
łőČý
2024ÖĐżź
ĄĄĄĄĄĄ ĄĄĄĄ
ĄĄĄĄĄĄ ĄĄĄĄ
ĄĄĄĄĄĄ ĄĄĄĄ
ĄĄĄĄĄĄ ĄĄĄĄ
ĄĄĄĄĄĄ ĄĄĄĄ
ĄĄĄĄĄĄ ĄĄĄĄ
- Ôî}ŁşŐZ(y¨ł)ÎÄŐćî} žÁî} ÔÂżź ĆÚÖĐ ĆÚÄŠ
- ÖŞ×Rüc(di¨Łn)Łşżźüc(di¨Łn)ˇÖÎö ×ÖŇô×ÖĐÎ Ô~ŐZ(y¨ł)˝âá ÎÄW(xu¨Ś)łŁ×R ÎÄŃÔÎÄ ŹF´úÎÄé×x
- Ôî}Łş ľW(xu¨Ś)Őćî} žÁî} ÔÂżź ĆÚÖĐ ĆÚÄŠ
- ÖŞ×Rüc(di¨Łn)Łşżźüc(di¨Łn)ˇÖÎö Čý˝ÇşŻľ Čý˝ÇĐÎ (sh¨Ş)ľ śţ´ÎşŻľ ŇťÔŞśţ´Îˇ˝łĚ A
ĄĄĄĄĄĄ ĄĄĄĄ
- Ôî}Łş ÎďŔíŐćî} žÁî} ÔÂżź ĆÚÖĐ ĆÚÄŠ
- ÖŞ×Rüc(di¨Łn)Łşżźüc(di¨Łn)ˇÖÎö šâľÄˇ´Éä şÁŚş ş(ji¨Łn)ÎCĐľ ë¡ĹcëÁ÷ Wġś¨ÂÉ
- Ôî}Łş ťŻW(xu¨Ś)Őćî} žÁî} ÔÂżź ĆÚÖĐ ĆÚÄŠ
- ÖŞ×Rüc(di¨Łn)Łşżźüc(di¨Łn)ˇÖÎö ËŽľÄłÉ ËáAű} ĚźľÄŃőťŻÎď ťŻW(xu¨Ś)ˇ˝łĚĘ˝ ČÜŇş
ĄĄĄĄĄĄ ĄĄĄĄ
ĄĄĄĄĄĄ ĄĄĄĄ
ĄĄĄĄĄĄ ĄĄĄĄ