1.▌Sī”ĘQ(ch©źng)Ą─Č©
░čę╗éĆ(g©©)łDą╬čžų°(zh©┤)─│ę╗Ślų▒ŠĆ(xi©żn)ĘŁš█���Ż¼╚ń╣¹╦³─▄ē“┼c┴Ēę╗éĆ(g©©)łDą╬ųž║Ž����Ż¼─Ū├┤ĘQ(ch©źng)▀@ā╔éĆ(g©©)łDą╬ĻP(gu©Īn)ė┌▀@Ślų▒ŠĆ(xi©żn)ī”ĘQ(ch©źng)���Ż¼ę▓ĘQ(ch©źng)▀@ā╔éĆ(g©©)łDą╬│╔▌Sī”ĘQ(ch©źng)��Ż¼▀@Ślų▒ŠĆ(xi©żn)Įąū÷ī”ĘQ(ch©źng)▌S����ĪŻš█»B║¾ųž║ŽĄ─³c(di©Żn)╩Ūī”欳c(di©Żn)�����Ż¼ę▓Įąū÷ī”ĘQ(ch©źng)³c(di©Żn)����ĪŻ
ĪŠ▌Sī”ĘQ(ch©źng)ųĖĄ─╩Ūā╔éĆ(g©©)łDą╬Ą─╬╗ų├ĻP(gu©Īn)ŽĄ�����Ż¼ā╔éĆ(g©©)łDą╬čžų°(zh©┤)─│Ślų▒ŠĆ(xi©żn)ī”š█║¾─▄ē“═Ļ╚½ųž║Ž.│╔▌Sī”ĘQ(ch©źng)Ą─ā╔éĆ(g©©)łDą╬ę╗Č©╚½Ą╚���Ī�����ŻĪ┐
2.▌Sī”ĘQ(ch©źng)łDą╬Ą─Č©┴x
░čę╗éĆ(g©©)łDą╬čžų°(zh©┤)─│ų▒ŠĆ(xi©żn)š█»B��Ż¼╚ń╣¹ų▒ŠĆ(xi©żn)ā╔┼įĄ─▓┐Ęų─▄╗źŽÓųž║Ž��Ż¼─Ū├┤▀@éĆ(g©©)łDą╬╩Ū▌Sī”ĘQ(ch©źng)łDą╬�Ż¼▀@Ślų▒ŠĆ(xi©żn)Š═╩Ūī”ĘQ(ch©źng)▌S����ĪŻ
ĪŠ▌Sī”ĘQ(ch©źng)łDą╬╩ŪųĖę╗éĆ(g©©)łDą╬���Ż¼łDą╬▒╗ī”ĘQ(ch©źng)▌SĘų│╔Ą─ā╔▓┐Ęų─▄ē“╗źŽÓųž║Ž.ę╗éĆ(g©©)▌Sī”ĘQ(ch©źng)łDą╬Ą─ī”ĘQ(ch©źng)▌S▓╗ę╗Č©ų╗ėąę╗Śl��Ż¼ę▓┐╔─▄ėąā╔Śl╗“ČÓŚl�Ż¼ę“łDą╬Č°Č©��Ī��ŻĪ┐
3.▌Sī”ĘQ(ch©źng)┼c▌Sī”ĘQ(ch©źng)łDą╬Ą─ģ^äe┼c┬ō(li©ón)ŽĄ
▌Sī”ĘQ(ch©źng)┼c▌Sī”ĘQ(ch©źng)łDą╬Ą─ų„ę¬ģ^äeŻ║▌Sī”ĘQ(ch©źng)╩ŪųĖā╔éĆ(g©©)łDą╬���Ż¼Č°▌Sī”ĘQ(ch©źng)łDą╬╩Ūę╗éĆ(g©©)łDą╬;▌Sī”ĘQ(ch©źng)łDą╬║═▌Sī”ĘQ(ch©źng)Ą─ĻP(gu©Īn)ŽĄĘŪ│Ż├▄Ūą����Ż¼╚¶░č│╔▌Sī”ĘQ(ch©źng)Ą─ā╔éĆ(g©©)łDą╬┐┤ū„ę╗éĆ(g©©)š¹¾w�����Ż¼ät▀@éĆ(g©©)š¹¾wŠ═╩Ū▌Sī”ĘQ(ch©źng)łDą╬;Ę┤▀^(gu©░)üĒ(l©ói)���Ż¼╚¶░č▌Sī”ĘQ(ch©źng)łDą╬Ą─ī”ĘQ(ch©źng)▌Sā╔┼įĄ─▓┐Ęų┐┤ū„ā╔éĆ(g©©)łDą╬��Ż¼ät▀@ā╔éĆ(g©©)łDą╬ĻP(gu©Īn)ė┌▀@Ślų▒ŠĆ(xi©żn)(įŁī”ĘQ(ch©źng)▌S)ī”ĘQ(ch©źng).���ĪŻ
4.▌Sī”ĘQ(ch©źng)Ą─ąį┘|(zh©¼)
▌Sī”ĘQ(ch©źng)Ą─ąį┘|(zh©¼)Ż║│╔▌Sī”ĘQ(ch©źng)Ą─ā╔éĆ(g©©)łDą╬ųą��Ż¼ī”欳c(di©Żn)Ą─▀BŠĆ(xi©żn)▒╗ī”ĘQ(ch©źng)▌S┤╣ų▒ŲĮĘų;│╔▌Sī”ĘQ(ch©źng)Ą─ā╔éĆ(g©©)łDą╬Ą─╚╬║╬ī”æ¬▓┐Ęųę▓│╔▌Sī”ĘQ(ch©źng);│╔▌Sī”ĘQ(ch©źng)Ą─ā╔éĆ(g©©)łDą╬╚½Ą╚���ĪŻ
5.ŠĆ(xi©żn)Č╬Ą─▌Sī”ĘQ(ch©źng)ąį
ó┘ŠĆ(xi©żn)Č╬╩Ū▌Sī”ĘQ(ch©źng)łDą╬���Ż¼ŠĆ(xi©żn)Č╬Ą─┤╣ų▒ŲĮĘųŠĆ(xi©żn)╩Ū╦³Ą─ī”ĘQ(ch©źng)▌S����ĪŻ
ó┌ŠĆ(xi©żn)Č╬┤╣ų▒ŲĮĘųŠĆ(xi©żn)Ą─ąį┘|(zh©¼)Č©└ĒŻ║ŠĆ(xi©żn)Č╬┤╣ų▒ŲĮĘųŠĆ(xi©żn)╔ŽĄ─³c(di©Żn)ĄĮŠĆ(xi©żn)Č╬ā╔Č╦Ą─ŠÓļxŽÓĄ╚��ĪŻ
ó█ŠĆ(xi©żn)Č╬┤╣ų▒ŲĮĘųŠĆ(xi©żn)Ą─ąį┘|(zh©¼)Č©└ĒĄ──µČ©└ĒŻ║ĄĮŠĆ(xi©żn)Č╬ā╔éĆ(g©©)Č╦ŠÓļxŽÓĄ╚Ą─³c(di©Żn)į┌ŠĆ(xi©żn)Č╬Ą─┤╣ų▒ŲĮĘųŠĆ(xi©żn)╔Ž�ĪŻ
ĪŠó┘ŠĆ(xi©żn)Č╬Ą─┤╣ų▒ŲĮĘųŠĆ(xi©żn)�����Ż¼«ŗ(hu©ż)│÷ĄĮŠĆ(xi©żn)Č╬ā╔éĆ(g©©)Č╦³c(di©Żn)Ą─ŠÓļx��Ż¼▀@śėŠ═│÷¼FŽÓĄ╚ŠĆ(xi©żn)Č╬�����Ż¼ų▒Įė╗“ķgĮėĄž×ķśŗįņ╚½Ą╚╚²ĮŪą╬äō(chu©żng )įņŚl╝■�����ĪŻó┌╚²ĮŪą╬╚²▀ģ┤╣ų▒ŲĮĘųŠĆ(xi©żn)Į╗ė┌ę╗³c(di©Żn)�����Ż¼įō³c(di©Żn)ĄĮ╚²ĮŪą╬╚²Ēö³c(di©Żn)Ą─ŠÓļxŽÓĄ╚�����Ż¼▀@³c(di©Żn)╩Ū╚²ĮŪą╬═ŌĮėłAĄ─łAą─——═Ōą─����Ī�����ŻĪ┐
6.ŠĆ(xi©żn)Č╬Ą─┤╣ų▒ŲĮĘųŠĆ(xi©żn)
┤╣ų▒▓óŪęŲĮĘųę╗ŚlŠĆ(xi©żn)Č╬Ą─ų▒ŠĆ(xi©żn)����Ż¼Įąū÷▀@ŚlŠĆ(xi©żn)Č╬Ą─┤╣ų▒ŲĮĘųŠĆ(xi©żn)��Ż¼ę▓ĮąŠĆ(xi©żn)Č╬Ą─ųą┤╣ŠĆ(xi©żn)�ĪŻ
7.ĮŪĄ─▌Sī”ĘQ(ch©źng)ąį
(1)ĮŪ╩Ū▌Sī”ĘQ(ch©źng)łDą╬�Ż¼ĮŪĄ─ŲĮĘųŠĆ(xi©żn)╦∙į┌Ą─ų▒ŠĆ(xi©żn)╩Ū╦³Ą─ī”ĘQ(ch©źng)▌S�ĪŻ
(2)ĮŪŲĮĘųŠĆ(xi©żn)╔ŽĄ─³c(di©Żn)ĄĮĮŪā╔▀ģĄ─ŠÓļxŽÓĄ╚���ĪŻ
(3)ĮŪĄ─ā╚▓┐ĄĮĮŪā╔▀ģŠÓļxŽÓĄ╚Ą─³c(di©Żn)į┌ĮŪĄ─ŲĮĘųŠĆ(xi©żn)╔Ž���ĪŻ
ĪŠó┘ė├Ę¹╠¢šZ(y©│)čį▒Ē╩ŠĮŪŲĮĘųŠĆ(xi©żn)╔ŽĄ─³c(di©Żn)ĄĮĮŪā╔▀ģĄ─ŠÓļxŽÓĄ╚��ĪŻ╚¶CDŲĮĘų∠ADB���Ż¼³c(di©Żn)P╩ŪCD╔Žę╗³c(di©Żn)����Ż¼ŪęPE⊥ADė┌³c(di©Żn)E��Ż¼PF⊥BDė┌³c(di©Żn)F����Ż¼ätPE=PFĪ┐
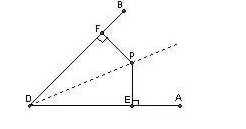
ĪŠó┌ė├Ę¹╠¢šZ(y©│)čį▒Ē╩ŠĮŪĄ─ā╚▓┐ĄĮĮŪā╔▀ģŠÓļxŽÓĄ╚Ą─³c(di©Żn)į┌ĮŪĄ─ŲĮĘųŠĆ(xi©żn)╔Ž��ĪŻ╚¶PE⊥ADė┌³c(di©Żn)E��Ż¼PF⊥BDė┌³c(di©Żn)F���Ż¼PE=PF�����Ż¼ätPDŲĮĘų∠ADB Ī┐
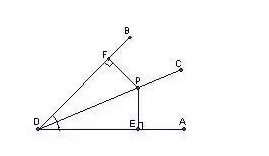
8.ĮŪŲĮĘųŠĆ(xi©żn)Ą─«ŗ(hu©ż)Ę©
ĮŪŲĮĘųŠĆ(xi©żn)Ą─│▀ęÄū„łD

·šµŅ}ĮŌ╬÷
┐╝³c(di©Żn)1 ┼ąäe▌Sī”ĘQ(ch©źng)łDą╬
└²1
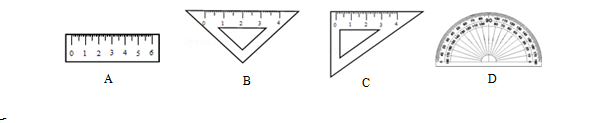
(2013─ĻŽ╠īÄ)Ž┬┴ąīW(xu©”)┴Ģė├Š▀ųą�����Ż¼▓╗╩Ū▌Sī”ĘQ(ch©źng)łDą╬Ą─╩Ū( ĪĪ)
Ęų╬÷
Ż║Ė∙ō■▌Sī”ĘQ(ch©źng)łDą╬Ą─Ė┼─ŅŻ║░čę╗éĆ(g©©)łDą╬čžę╗Ślų▒ŠĆ(xi©żn)š█»B���Ż¼ų▒ŠĆ(xi©żn)ā╔┼įĄ─▓┐Ęų─▄ē“╗źŽÓųž║ŽĄ─łDą╬╩Ū▌Sī”ĘQ(ch©źng)łDą╬����Ż¼ī”Ė„▀xĒŚųę╗┼ąöÓ╝┤┐╔��ĪŻ
ĮŌŻ║
▀xĒŚA����ĪóB����ĪóD╩Ū▌Sī”ĘQ(ch©źng)łDą╬�����Ż¼▀xĒŚC▓╗╩Ū▌Sī”ĘQ(ch©źng)łDą╬���Ż¼╣╩▀xC���ĪŻ
┐╝³c(di©Żn)2 ŠĆ(xi©żn)Č╬Ą─┤╣ų▒ŲĮĘųŠĆ(xi©żn)Ą─ąį┘|(zh©¼)
└²2
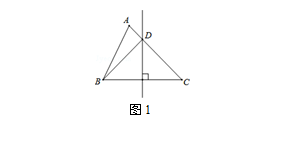
(2013─Ļ╠®ų▌)╚ńłD1����Ż¼į┌Ī„ABCųą����Ż¼AB+AC=6 cm�Ż¼BCĄ─┤╣ų▒ŲĮĘųŠĆ(xi©żn)l┼cACŽÓĮ╗ė┌³c(di©Żn)D���Ż¼ätĪ„ABDĄ─ų▄ķL(ch©óng)×ķĪĪĪĪcm.
Ęų╬÷Ż║
Ė∙ō■ŠĆ(xi©żn)Č╬┤╣ų▒ŲĮĘųŠĆ(xi©żn)Ą─ąį┘|(zh©¼)�����Ż¼┐╔Ą├DC=DB�����Ż¼▀M(j©¼n)Č°┐╔┤_Č©Ī„ABDĄ─ų▄ķL(ch©óng)���ĪŻ
ĮŌŻ║
ę“×ķl┤╣ų▒ŲĮĘųBC��Ż¼╦∙ęįDB=DC
╦∙ęįĪ„ABDĄ─ų▄ķL(ch©óng)=AB+AD+BD=AB+AD+DC=AB+AC=6 cm.╣╩╠Ņ6���ĪŻ
┐╝³c(di©Żn)3 «ŗ(hu©ż)▌Sī”ĘQ(ch©źng)łDą╬
└²3
(2013─Ļ╣■Ā¢×I)╚ńłD2╦∙╩Š����Ż¼į┌├┐éĆ(g©©)ąĪš²ĘĮą╬Ą─▀ģķL(ch©óng)Š∙×ķ1éĆ(g©©)å╬╬╗ķL(ch©óng)Č╚Ą─ĘĮĖ±╝łųą���Ż¼ėąŠĆ(xi©żn)Č╬AB║═ų▒ŠĆ(xi©żn)MN���Ż¼³c(di©Żn)A��Ż¼B�Ż¼M��Ż¼NŠ∙į┌ąĪš²ĘĮą╬Ą─Ēö³c(di©Żn)╔Ž�Ż¼į┌ĘĮĖ±╝łųą«ŗ(hu©ż)╦─▀ģą╬ABCD(╦─▀ģą╬Ą─Ė„Ēö³c(di©Żn)Š∙į┌ąĪš²ĘĮą╬Ą─Ēö³c(di©Żn)╔Ž)�Ż¼╩╣╦─▀ģą╬ABCD╩Ūęįų▒ŠĆ(xi©żn)MN×ķī”ĘQ(ch©źng)▌SĄ─▌Sī”ĘQ(ch©źng)łDą╬�����Ż¼³c(di©Żn)AĄ─ī”ĘQ(ch©źng)³c(di©Żn)×ķ³c(di©Żn)D���Ż¼³c(di©Żn)BĄ─ī”ĘQ(ch©źng)³c(di©Żn)×ķ³c(di©Żn)C��ĪŻ
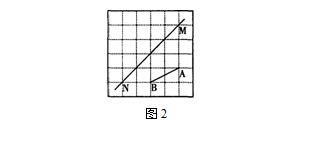
Ęų╬÷Ż║
▀^(gu©░)³c(di©Żn)A«ŗ(hu©ż)ų▒ŠĆ(xi©żn)MNĄ─┤╣ŠĆ(xi©żn)����Ż¼┤╣ūŃ×ķO����Ż¼į┌┤╣ŠĆ(xi©żn)╔ŽĮž╚ĪOD=OA��Ż¼DŠ═╩ŪAĻP(gu©Īn)ė┌ų▒ŠĆ(xi©żn)MNĄ─ī”ĘQ(ch©źng)³c(di©Żn);═¼└Ē��Ż¼«ŗ(hu©ż)│÷³c(di©Żn)BĻP(gu©Īn)ė┌ų▒ŠĆ(xi©żn)MNĄ─ī”ĘQ(ch©źng)³c(di©Żn)C;▀BĮėBC�Ż¼CD����Ż¼DA���Ż¼╝┤┐╔Ą├ĄĮ╦─▀ģą╬ABCD����ĪŻ
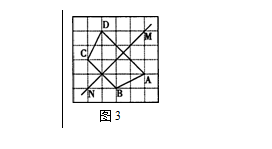
ĮŌŻ║
š²┤_«ŗ(hu©ż)łD╚ńłD3╦∙╩Š�����ĪŻ
└²4
(2013─Ļųžæc)ū„łDŅ}Ż║(▓╗ę¬Ū¾īæ(xi©¦)ū„Ę©)╚ńłD4╦∙╩Š��Ż¼Ī„ABCį┌ŲĮ├µų▒ĮŪū°ś╦ŽĄųą�Ż¼³c(di©Żn)A�Ż¼B���Ż¼CĄ─ū°ś╦Ęųäe×ķA(-2��Ż¼1)����Ż¼B(-4��Ż¼5)����Ż¼C(-5����Ż¼2)�ĪŻ
ó┼ū„Ī„ABCĻP(gu©Īn)ė┌ų▒ŠĆ(xi©żn)lŻ║x=-1ī”ĘQ(ch©źng)Ą─Ī„A1B1C1�Ż¼Ųõųą���Ż¼³c(di©Żn)A�Ż¼B�Ż¼CĄ─ī”欳c(di©Żn)Ęųäe×ķA1�Ż¼B1���Ż¼C1;
óŲīæ(xi©¦)│÷³c(di©Żn)A1�����Ż¼B1����Ż¼C1Ą─ū°ś╦����ĪŻ
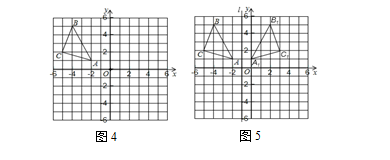
Ęų╬÷Ż║
ó┼Ė∙ō■ŠW(w©Żng)Ė±ĮYśŗšę│÷³c(di©Żn)A���Ż¼B���Ż¼CĻP(gu©Īn)ė┌ų▒ŠĆ(xi©żn)lĄ─ī”ĘQ(ch©źng)³c(di©Żn)A1�Ż¼B1�Ż¼C1�����Ż¼╚╗║¾Ēś┤╬▀BĮė╝┤┐╔;óŲų▒ĮėĖ∙ō■ŲĮ├µų▒ĮŪū°ś╦ŽĄīæ(xi©¦)│÷³c(di©Żn)A1���Ż¼B1����Ż¼C1Ą─ū°ś╦��ĪŻ
ĮŌŻ║
ó┼«ŗ(hu©ż)Ī„A1B1C1╚ńłD5╦∙╩Š�ĪŻ
óŲA1(0�����Ż¼1)�����ĪóB1(2��Ż¼5)����ĪóC1(3�����Ż¼2)����ĪŻ
┐╝³c(di©Żn)4 ĻP(gu©Īn)ė┌x▌S╗“y▌Sī”ĘQ(ch©źng)Ą─³c(di©Żn)Ą─ū°ś╦
└²5
(2013─Ļ╦ņīÄ)īó³c(di©Żn)A(3�����Ż¼2)čžx▌SŽ“ū¾ŲĮęŲ4éĆ(g©©)å╬╬╗ķL(ch©óng)Č╚Ą├ĄĮ³c(di©Żn)A′����Ż¼³c(di©Żn)A′ĻP(gu©Īn)ė┌y▌Sī”ĘQ(ch©źng)Ą─³c(di©Żn)Ą─ū°ś╦╩Ū(ĪĪĪĪ)
A.(-3����Ż¼2) B.(-1�����Ż¼2) C.(1����Ż¼2) D.(-1�����Ż¼-2)
Ęų╬÷Ż║
Ž╚└¹ė├ŲĮęŲųą³c(di©Żn)Ą─ūā╗»ęÄ┬╔Ū¾│÷³c(di©Żn)A′Ą─ū°ś╦���Ż¼į┘Ė∙ō■ĻP(gu©Īn)ė┌y▌Sī”ĘQ(ch©źng)Ą─³c(di©Żn)Ą─ū°ś╦╠žš„╝┤┐╔Ū¾ĮŌ����ĪŻ
ĮŌŻ║
ę“×ķīó³c(di©Żn)A(3�����Ż¼2)čžx▌SŽ“ū¾ŲĮęŲ4éĆ(g©©)å╬╬╗ķL(ch©óng)Č╚Ą├ĄĮ³c(di©Żn)A′�����Ż¼╦∙ęį³c(di©Żn)A′Ą─ū°ś╦×ķ(-1���Ż¼2)���ĪŻ╦∙ęį³c(di©Żn)A′ĻP(gu©Īn)ė┌y▌Sī”ĘQ(ch©źng)Ą─³c(di©Żn)Ą─ū°ś╦╩Ū(1�Ż¼2)�����Ż¼╣╩▀xC���ĪŻ
┐╝³c(di©Żn)5 Ą╚č³╚²ĮŪą╬Ą─ąį┘|(zh©¼)
└²6
(2013─Ļ┼_×│)╚ńłD6���Ż¼į┌ķL(ch©óng)ĘĮą╬ABCDųą�Ż¼M×ķCDųą³c(di©Żn)��Ż¼ĘųäeęįB�����Ż¼M×ķłAą─�Ż¼BC�����Ż¼MCķL(ch©óng)×ķ░ļÅĮ«ŗ(hu©ż)╗Ī���Ż¼ā╔╗ĪŽÓĮ╗ė┌³c(di©Żn)P���ĪŻ╚¶∠PBC=70°�Ż¼ät∠MPCĄ─Č╚öĄ×ķ(ĪĪ )
A.20° B.35° C.40° D.55°
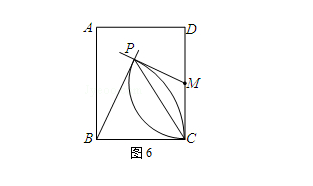
Ęų╬÷Ż║
Ė∙ō■Ą╚č³╚²ĮŪą╬ā╔ĄūĮŪŽÓĄ╚Ū¾│÷∠BCP����Ż¼╚╗║¾Ū¾│÷∠MCP�����Ż¼į┘Ė∙ō■“Ą╚▀ģī”Ą╚ĮŪ”Ū¾ĮŌ╝┤┐╔.
ĮŌŻ║
ę“×ķĘųäeęįB���Ż¼M×ķłAą─�����Ż¼BC���Ż¼MCķL(ch©óng)×ķ░ļÅĮĄ─ā╔╗ĪŽÓĮ╗ė┌³c(di©Żn)P�Ż¼╦∙ęįBP=BC���Ż¼MP=MC���ĪŻ
ę“×ķ∠PBC=70°��Ż¼╦∙ęį∠BCP=1/2(180°-∠PBC)=1/2(180°-70°)=55°
į┌ķL(ch©óng)ĘĮą╬ABCDųą��Ż¼∠BCD=90°�����Ż¼╦∙ęį∠MCP=90°-∠BCP=90°-55°=35°
╦∙ęį∠MPC=∠MCP=35°��Ż¼╣╩▀xB���ĪŻ
┐╝³c(di©Żn)6 Ą╚▀ģ╚²ĮŪą╬Ą─ąį┘|(zh©¼)
└²7
(2013─ĻŪŁ╬„─Žų▌)╚ńłD8��Ż¼ęčų¬Ī„ABC╩ŪĄ╚▀ģ╚²ĮŪą╬�Ż¼³c(di©Żn)B�����Ż¼C��Ż¼D����Ż¼Eį┌═¼ę╗ų▒ŠĆ(xi©żn)╔Ž�����Ż¼ŪęCG=CD��Ż¼DF=DE�����Ż¼ät∠EĄ─Č╚öĄ×ķ
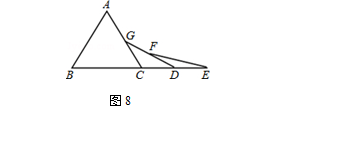
Ęų╬÷Ż║
Ė∙ō■Ą╚▀ģ╚²ĮŪą╬Ą─ąį┘|(zh©¼)����Ż¼┐╔ų¬∠ACB=60°�����Ż¼Ė∙ō■Ą╚č³╚²ĮŪą╬ĄūĮŪŽÓĄ╚╝┤┐╔Ą├│÷∠EĄ─Č╚öĄ�ĪŻ
ĮŌŻ║
ę“×ķĪ„ABC╩ŪĄ╚▀ģ╚²ĮŪą╬���Ż¼╦∙ęį∠ACB=60°����Ż¼∠ACD=120°
ę“×ķCG=CD�����Ż¼╦∙ęį∠CDG=30°��Ż¼∠FDE=150°
ę“×ķDF=DE�Ż¼╦∙ęį∠E=15°��Ż¼╣╩╠Ņ15°
┐╝³c(di©Żn)7║¼300ĮŪĄ─ų▒ĮŪ╚²ĮŪą╬Ą─ąį┘|(zh©¼)
└²8
(2013─Ļ╠®░▓)╚ńłD9�����Ż¼į┌RtĪ„ABCųą�����Ż¼∠ACB=90°��Ż¼ABĄ─┤╣ų▒ŲĮĘųŠĆ(xi©żn)DEĮ╗ACė┌³c(di©Żn)E�Ż¼Į╗BCĄ─čėķL(ch©óng)ŠĆ(xi©żn)ė┌³c(di©Żn)F�����Ż¼╚¶∠F=30°��Ż¼DE=1�Ż¼ätBEĄ─ķL(ch©óng)╩Ū
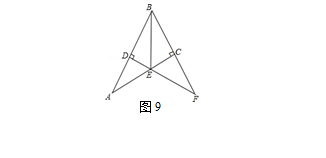
Ęų╬÷Ż║
Ė∙ō■Ņ}ęŌ═ŲĄ├∠DBE=30°�����Ż¼ätį┌RtĪ„DBEųąė╔“30°ĮŪ╦∙ī”Ą─ų▒ĮŪ▀ģ╩Ūą▒▀ģĄ─ę╗░ļ”╝┤┐╔Ū¾Ą├ŠĆ(xi©żn)Č╬BEĄ─ķL(ch©óng)Č╚��ĪŻ
ĮŌŻ║
ę“×ķFD⊥AB��Ż¼╦∙ęį∠ACB=∠FDB=90°
ę“×ķ∠F=30°����Ż¼╦∙ęį∠A=∠F=30°
ėųDE┤╣ų▒ŲĮĘųŠĆ(xi©żn)AB����Ż¼╦∙ęį∠EBA=∠A=30°
ę“×ķDE=1���Ż¼╦∙ęįBE=2DE=2�����Ż¼╣╩╠Ņ2��ĪŻ
·š`ģ^³c(di©Żn)ō▄
š`ģ^1 ▌Sī”ĘQ(ch©źng)║¼┴x└ĒĮŌ▓╗ŪÕų┬Õe
└²1
╚ńłD1ųąĄ─(1)����Īó(2)ā╔éĆ(g©©)łDą╬│╔▌Sī”ĘQ(ch©źng)��Ż¼šł«ŗ(hu©ż)│÷╦³éāĄ─ī”ĘQ(ch©źng)▌S��ĪŻ
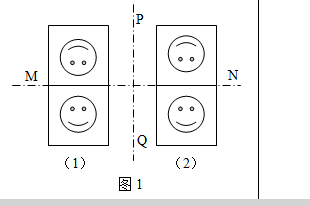
ÕeĮŌŻ║
╚ńłD1╦∙╩ŠĄ─ų▒ŠĆ(xi©żn)MN
Ų╩╬÷Ż║
čžų▒ŠĆ(xi©żn)MNī”š█��Ż¼į┌ų▒ŠĆ(xi©żn)MNā╔┼įĄ─łDą╬Ą─┤_┐╔ęį╗źŽÓųž║Ž�����Ż¼Ą½▀@└’ę¬Ū¾Ą─╩Ū«ŗ(hu©ż)(1)�Īó(2)Ą─ī”ĘQ(ch©źng)▌S��Ż¼Č°MN▓ó▓╗╩Ū▀@ā╔éĆ(g©©)łDą╬Ą─ī”ĘQ(ch©źng)▌S���ĪŻ«ŗ(hu©ż)│╔▌Sī”ĘQ(ch©źng)Ą─ā╔éĆ(g©©)łDą╬Ą─ī”ĘQ(ch©źng)▌SĢr(sh©¬)ę¬ūóęŌ╦∙ųĖĄ─╩Ū──éĆ(g©©)ā╔éĆ(g©©)łDą╬���Ż¼╠žäeūóęŌ«ö▀@ā╔éĆ(g©©)łDą╬▒Š╔Ēę▓╩Ū▌Sī”ĘQ(ch©źng)łDą╬Ģr(sh©¬)�Ż¼▓╗ę¬░čĖ„ūįłDą╬Ą─ī”ĘQ(ch©źng)▌Sū„×ķā╔éĆ(g©©)łDą╬Ą─ī”ĘQ(ch©źng)▌S�����ĪŻ
š²ĮŌŻ║
╚ńłD1╦∙╩ŠĄ─ų▒ŠĆ(xi©żn)PQ
š`ģ^2
└²2
╚ńłD2����Ż¼ęčų¬A�����Ż¼Cā╔³c(di©Żn)ĻP(gu©Īn)ė┌BDī”ĘQ(ch©źng)��Ż¼Ž┬┴ąĮYšōŻ║ó┘OA=OC;ó┌OB=OD;ó█AD=CD;ó▄AB=CB��ĪŻŲõųąš²┤_Ą─ėą (╠Ņą“╠¢╝┤┐╔).
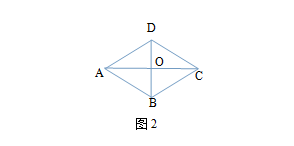
ÕeĮŌŻ║
╠Ņó┘ó┌ó█ó▄.
Ų╩╬÷Ż║
ÕeĮŌ“A�����Ż¼Cā╔³c(di©Żn)ĻP(gu©Īn)ė┌BDī”ĘQ(ch©źng)”Õeš`└ĒĮŌ×ķ“AC�Ż¼BD╗źŽÓ┤╣ų▒ŲĮĘų”��Ż¼īŹ(sh©¬)ļH╔ŽOA=OC�����Ż¼AB=CB����Ż¼AD=CD│╔┴ó����Ż¼Ą½OB=OD▓╗ę╗Č©│╔┴ó�����ĪŻ
š²ĮŌŻ║
╠Ņó┘ó█ó▄.
ŠÄ▌ŗ═Ų╦]Ż║
2023─Ļųą┐╝Ė„┐Ų─┐ųž³c(di©Żn)ų¬ūRģR┐é
ĪĪĪĪūŅą┬ųą┐╝┘YėŹ���Īóųą┐╝š■▓▀����Īó┐╝Ū░£╩éõ���Īóųą┐╝ŅA£y�����Īóõø╚ĪĘųöĄŠĆ(xi©żn)Ą╚
ĪĪĪĪųą┐╝Ģr(sh©¬)ķgŠĆ(xi©żn)Ą─╚½▓┐ųžę¬╣سc(di©Żn)
ĪĪĪĪ▒Mį┌"ųą┐╝ŠW(w©Żng)"╬óą┼╣½▒Ŗ╠¢

ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC�����ĪóŲĮ░ÕĄ╚ęŲäė(d©░ng)įOéõįL(f©Żng)å¢(w©©n)ųą┐╝ŠW(w©Żng)�����Ż¼2023ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą����ŻĪ>>³c(di©Żn)ō¶▓ķ┐┤



















