一元二次方程的基本內容

現有一個(gè)長(cháng)方形寬為x米，長(cháng)比寬的2倍少3米，那么當面積為10平方米時(shí)寬是多少?

根據長(cháng)方形的面積公式我們能夠得到：(2x-3)·x=10，化簡(jiǎn)后，2x^2-3x-10=0。在數學(xué)中，我們把這類(lèi)式子叫做“一元二次方程”。

1、方程滿(mǎn)足的條件

●(1)等號兩邊都是整式

●(2)只含有一個(gè)未知數

●(3)未知數的最高次數是2的方程

2、方程的形式

一元二次方程的一般形式：ax2+bx+c=0(a≠0)，

特征：等式左邊加一個(gè)關(guān)于未知數x的二次多項式，等式右邊是零，其中ax2叫做二次項，a叫做二次項系數;bx叫做一次項，b叫做一次項系數;c叫做常數項。

3、方程的性質(zhì)

(1)一元二次方程根的判別式：當ax2+bx+c=0 (a≠0)時(shí)，Δ=b2-4ac 叫一元二次方程根的判別式。

當Δ>0 <=> 有兩個(gè)不等的實(shí)根;

當Δ=0 <=> 有兩個(gè)相等的實(shí)根;

當Δ<0 <=> 無(wú)實(shí)根。

注意：當Δ≥0 <=> 有兩個(gè)實(shí)根，需要根據題目要求，驗證這兩個(gè)實(shí)根是否相等。

(2)方程的兩根與方程系數的關(guān)系：x1+x2= -b/a，x1·x2=c/a，方程兩根為x1，x2時(shí)，方程為：x2+(x1+x2)X+x1x2=0。

一元二次方程的應用

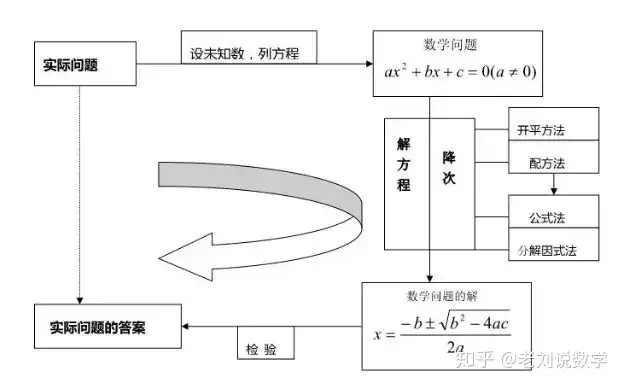
01、方程解法

一元二次方程的解是以降次為目的，以求解方法為主要手段，從而把一元二次方程轉化為一元一次方程求解。一元二次方程的一般解法有以下幾種：

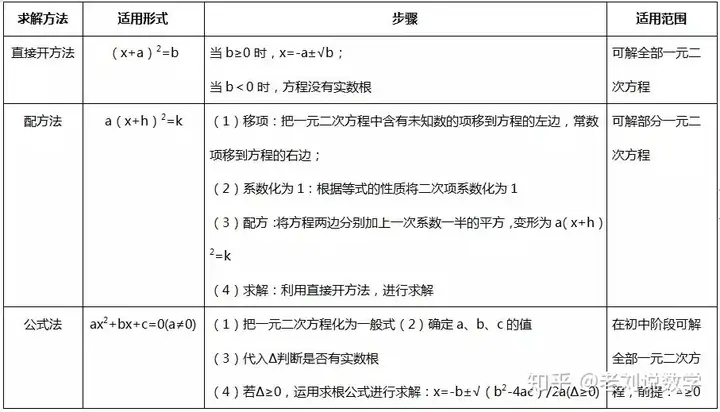
解一元二次方程時(shí)一般不使用配方法(除特別要求外)，但必須熟練掌握。解一元二次方程選擇方法的一般順序是：直接開(kāi)平方法→因式分解法→公式法→配方法。

02、根的判別式

利用一元二次方程根的判別式，確定方程字母系數的值時(shí)候，要注意二次項系數不為零這個(gè)隱含條件。

主要考察內容：

(1)不解方程，應用根的判別式，判斷一元二次方程根的情況

(2)已知方程中根的情況，如何由判別式逆推參數的取值范圍

(3)分類(lèi)討論：如果方程沒(méi)有支出二次方程和根的情況，一定要對方程進(jìn)行分類(lèi)討論，如果二次系數為0，方程可能是一元一次方程，如果二次項系數不為0，一元二次方程可能有兩個(gè)相等或不相等的實(shí)數根以及無(wú)實(shí)數根。

(4)一元二次方程根的判別式與整數解的綜合

03、實(shí)際問(wèn)題

列一元二次方程解實(shí)際應用的步驟：

審：審題目，分清已知量、未知量、等量關(guān)系

設：設未知數，有時(shí)會(huì )用未知數表示相關(guān)的量

列：根據題目中的等量關(guān)系，列出方程

解：解方程，注意分式方程需要檢驗，將所求量表示清晰

驗：檢驗方程的解是否滿(mǎn)足題目條件，注意要使其實(shí)際問(wèn)題有意義答：寫(xiě)出答案，切忌答非所問(wèn)

三類(lèi)常見(jiàn)問(wèn)題：

01、增長(cháng)率的等量關(guān)系

增長(cháng)率=(正常量/基礎量)*100%

設a為原來(lái)量，m為平均增長(cháng)率，n為增長(cháng)次數，b為增長(cháng)后的量，則a(1+m)n=b。當m為平均下降量時(shí)，n為下降次數，b為下降后的量，則有a(1-m)n=b。

02、利潤的等量關(guān)系

利潤=售價(jià)-成本

利潤率=(利潤/成本)*100%

這類(lèi)題的難點(diǎn)就在于同學(xué)不清楚價(jià)格變化和銷(xiāo)售量變化之間的關(guān)系，不管你運用哪種解題方法，能夠清晰解析出題目的各個(gè)變量之間的關(guān)系，才是重中之重。

03、幾何問(wèn)題等量關(guān)系

這類(lèi)問(wèn)題主要根據幾何圖形的性質(zhì)、特征、定理或公式等來(lái)尋找等量關(guān)系，常與三角形、四邊形、不等式(組)等知識綜合命題，解答時(shí)要在全面分析的前提下，注意合理運用代數式的變形技巧。

　　 歡迎使用手機、平板等移動(dòng)設備訪(fǎng)問(wèn)中考網(wǎng)，2024中考一路陪伴同行！>>點(diǎn)擊查看