在中考數學(xué)中三角形的考點(diǎn)一般會(huì )涉及到以下內容：

1、三角形的分類(lèi)、邊角關(guān)系及性質(zhì)。

2、三角形中幾條重要的線(xiàn)段及其性質(zhì)。(角平分線(xiàn)、中線(xiàn)、高線(xiàn)、垂直平分線(xiàn)、中位線(xiàn))

3、全等三角形的判定和性質(zhì)。全等三角形的判定和性質(zhì)是三角形部分的重點(diǎn)內容，一般三角形常用的有四種判定定理，直角三角形還需加上HL定理。除了需要掌握基本的性質(zhì)、判定、定理之外，全等三角形常用模型也必須要熟悉，像手拉手模型和一線(xiàn)三等角模型，在考試中出現的頻率比較高。

4、等腰三角形。等腰三角形的學(xué)習需要從定義、性質(zhì)和判定三方面去學(xué)習和掌握，等腰三角形的三線(xiàn)合一性質(zhì)是考試必考的內容，此外，在等腰三角中一定要有分類(lèi)討論意識，像在一些有關(guān)等腰三角形的幾何綜合題中，經(jīng)常需要運用分類(lèi)討論思想。

5、等邊三角形。等邊三角形是特殊的等腰三角形，具有等腰三角形所有的性質(zhì)，且三邊都相等，三角都為60°，在考試中經(jīng)常會(huì )考到其性質(zhì)。

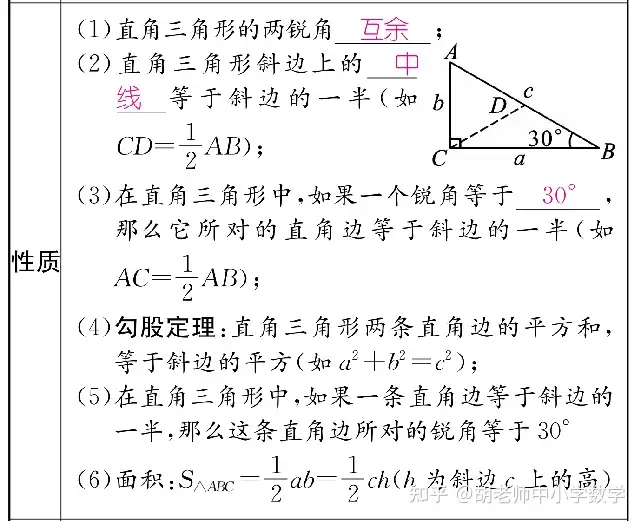
6、直角三角形。對于直角三角形的學(xué)習需要掌握幾大塊知識點(diǎn)，直角三角形的性質(zhì)、直角三角形的判定及初中幾何最重要的定理勾股定理，對直角三角形的所有的性質(zhì)定理和判定都必須要熟練掌握，像直角三角形斜邊上的中線(xiàn)等于斜邊的一半這條定理在考試中經(jīng)�？嫉�，但容易被學(xué)生所忽視。

除此之外還需掌握兩中特殊的三角形(含有45度的直角三角形和含有30度的直角三角形)的性質(zhì)，在解題中經(jīng)常需要運用到這兩種三角形的性質(zhì)，像經(jīng)常直接用在直角三角形中30°所對的直角邊是斜邊的一半這條性質(zhì)計算直角三角形的邊長(cháng)。

7、相似三角形。相似三角形的性質(zhì)及其判定是學(xué)習的重點(diǎn)，相似三角形、全等三角形及銳角三角形函數作為三角形的三大工具，在角度計算、邊長(cháng)計算及邊角關(guān)系的證明上有非常廣泛的用處，相對全等三角形，相似三角形的難度會(huì )略大一些，在中考會(huì )直接考查到利用相似測高或計算線(xiàn)段長(cháng)度，也會(huì )在四邊形、圓以及幾何綜合題中考查到相似。

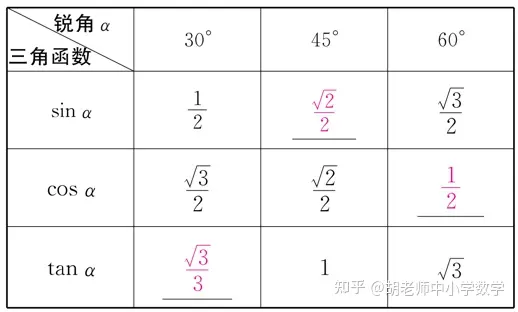
8、銳角三角形函數，對銳角三角函數的學(xué)習，需要掌握三種銳角三角函數的定義、特殊的三角函數值及銳角三角函數的應用，其中定義及特殊的三角函數值是基礎，應用是重點(diǎn)。

三角形作為中考必考的知識點(diǎn)，在考題上既有特別基礎的題，也有中等題，還有一些綜合題，在復習備考的過(guò)程中首先需要掌握知識要點(diǎn)和細節，了解考點(diǎn)、考向和題型，再幾何自身情況去做一些有針對性的練習題。

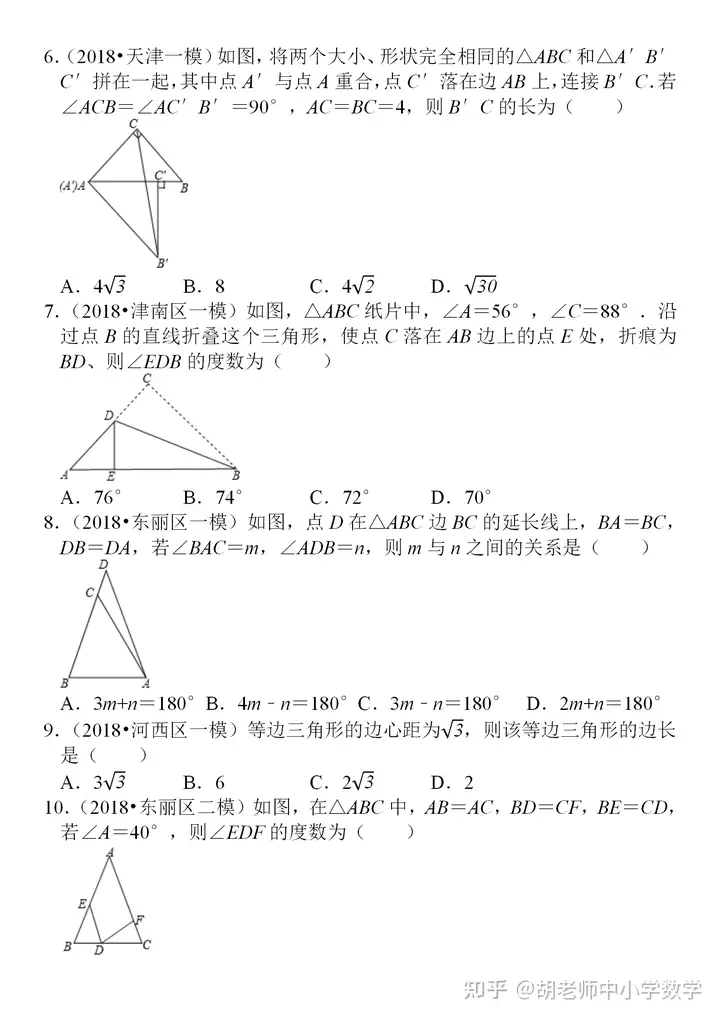
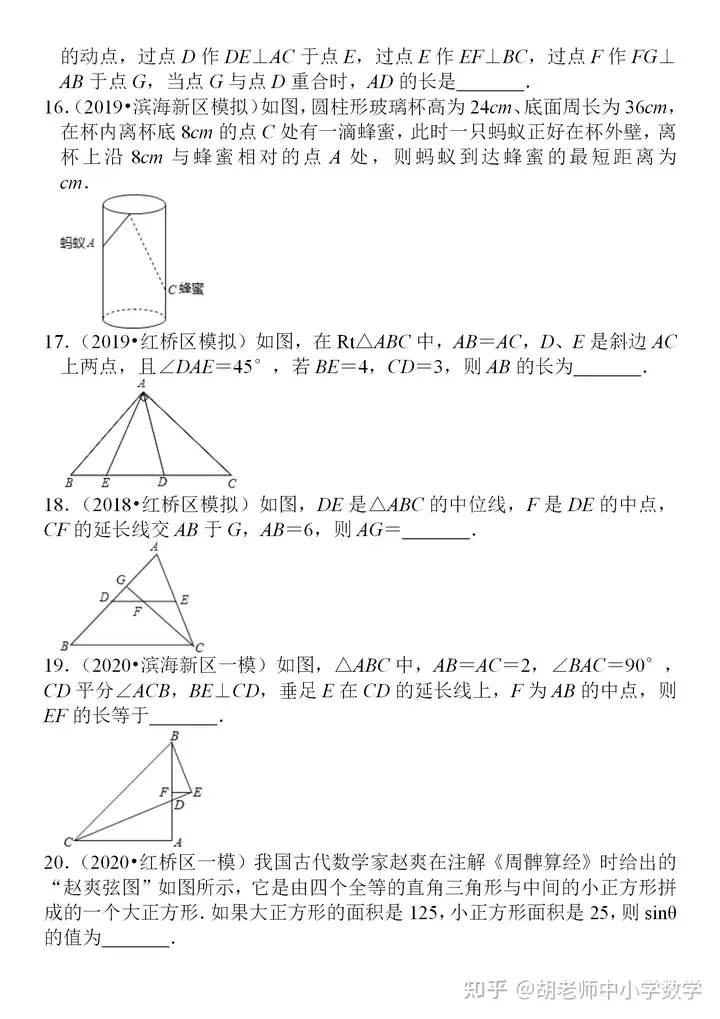
分享一份比較經(jīng)典的三角形練習題，這些題目均來(lái)自近三年某地各校的�？荚嚲�，拿到題目后我自己也完整做了一遍，發(fā)現這份題目質(zhì)量較高，幾何涵蓋了三角形的所有核心考點(diǎn)和題型，也包含著(zhù)一些常見(jiàn)的模型，很多題目還是具有一定的綜合性和難度，適合基礎中等及偏上的學(xué)生去練習，尤其是解答題的第三問(wèn)，很多都要求直接寫(xiě)出答案，但沒(méi)有正確的思路和完整的過(guò)程又怎會(huì )有正確的答案呢?第三問(wèn)大部分都是幾何綜合探究題，涉及到翻折、旋轉等圖形的變化，圖像更加抽象，很多時(shí)候需要自己去作圖、分析，然后尋找解題思路和方法，這些題目適合基礎比較扎實(shí)的一些同學(xué)來(lái)完成。

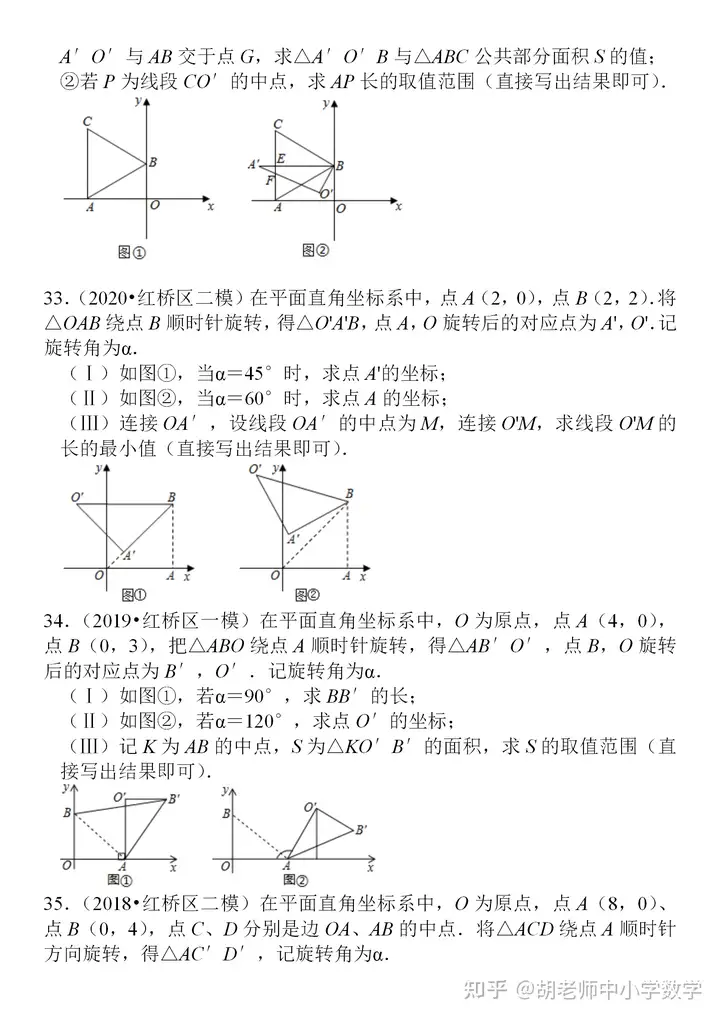
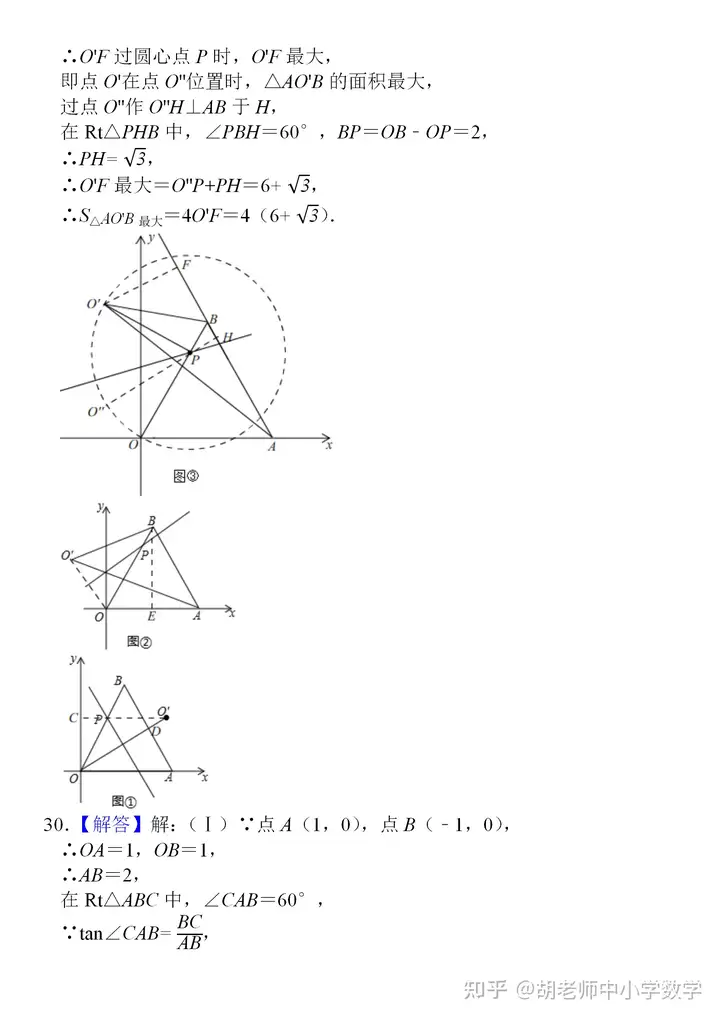
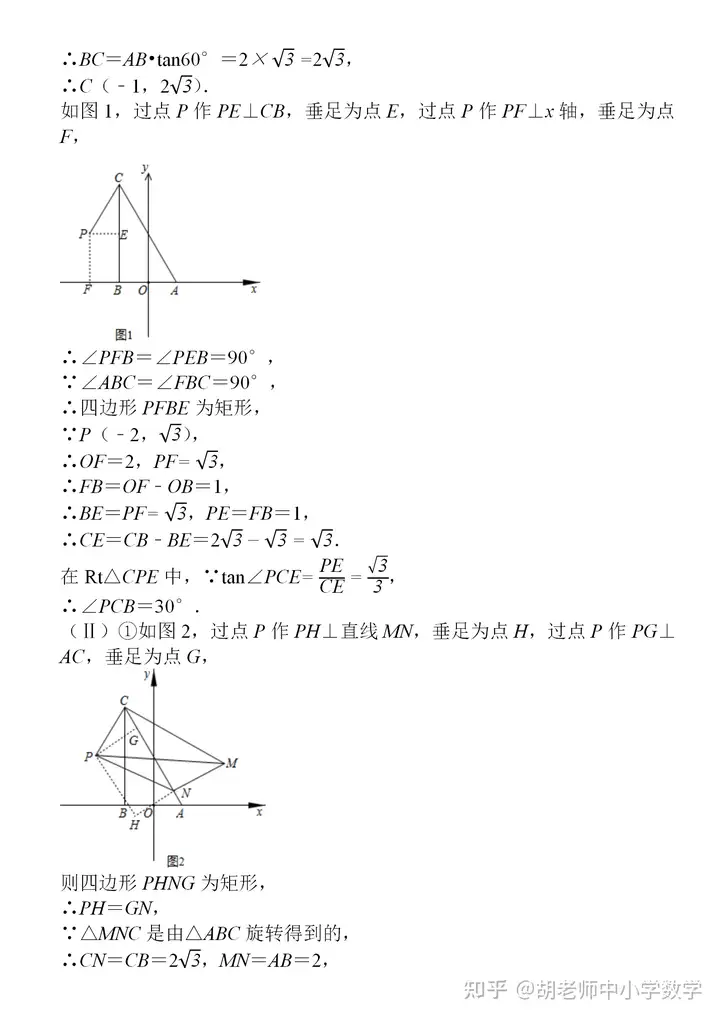
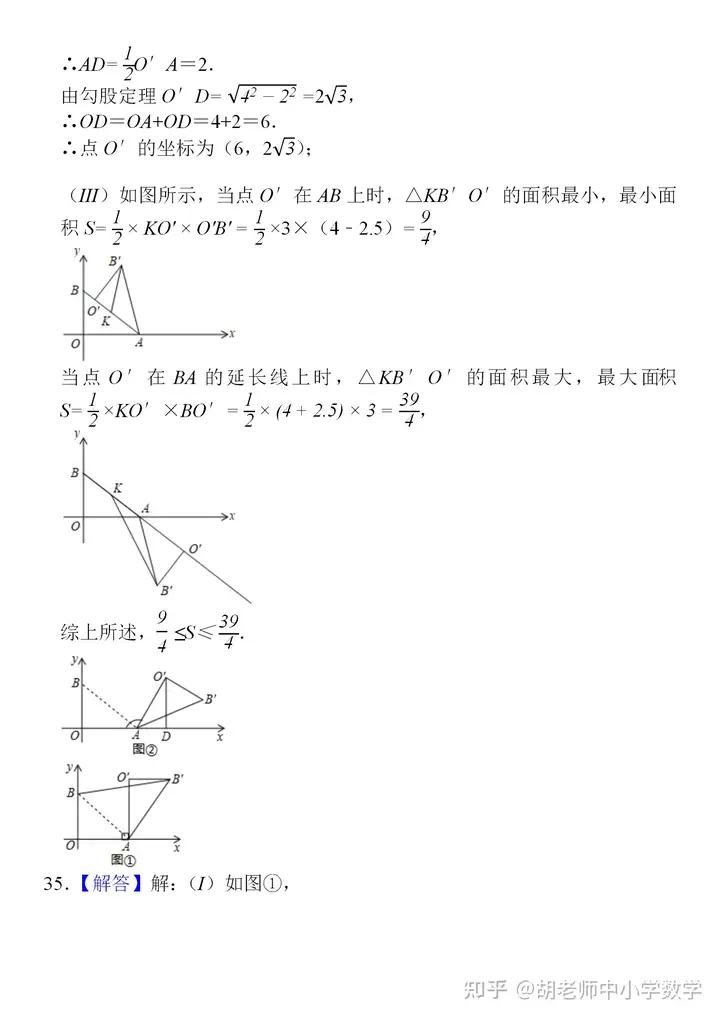
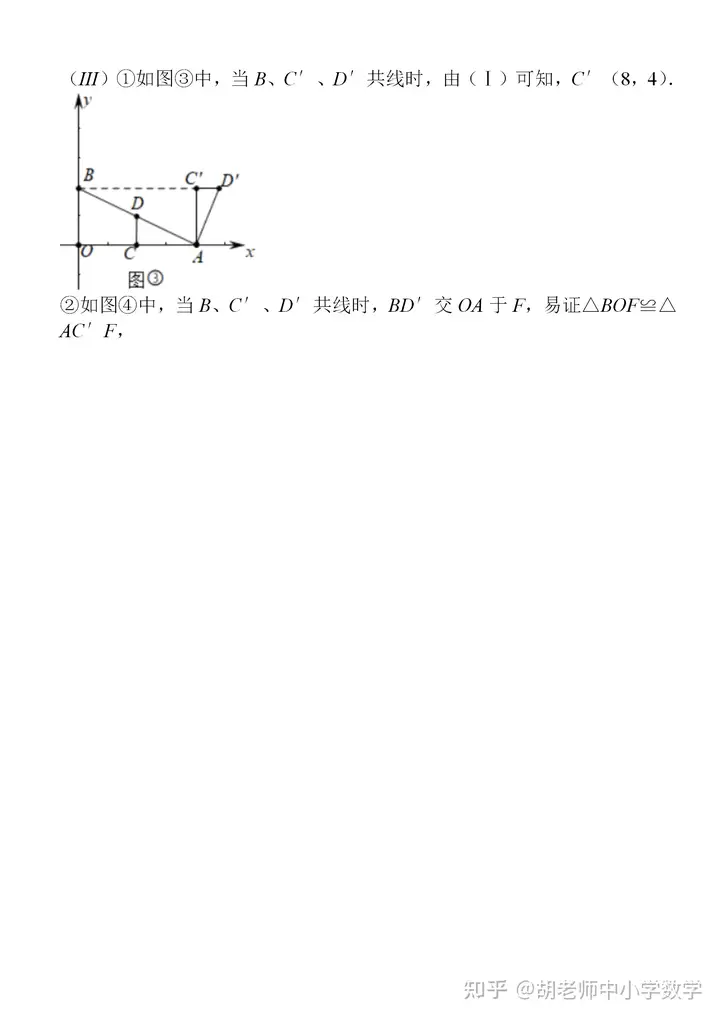
     編輯推薦：

      2023年中考各科目重點(diǎn)知識匯總