一次函數

1、定義：如果y=kx+b (k0 k,b是常量) ，那么y是x的一次函數。當b=0時(shí)，此時(shí)是正比例函數，是一次函數的一種特殊情況。

2、k值對于一次函數圖像的影響

當k>0時(shí)：y隨x的增大而增大，圖像為“/”的形式(上坡路);

當k<0時(shí)：y隨x的增大而減小，圖像為“\”的形式(下坡路)。

3、b值對于一次函數圖像的影響

當b>0時(shí)，圖像交于y軸的正半軸;

當b=0時(shí)，圖像是正比例函數，過(guò)原點(diǎn);

當b<0時(shí)，圖像交于y軸的負半軸。

4、直線(xiàn)與直線(xiàn)的位置關(guān)系

①平行：如果兩條直線(xiàn)平行，那么這兩條直線(xiàn)的k值相等，b值不等;

②垂直：如果兩條直線(xiàn)垂直，那么它們的k值相乘等于-1 。

反比例函數

1、定義：如果y=k/x (k≠0),那么y是x的反比例函數。

2、k值對于反比例函數圖像的影響

①當k>0時(shí)：雙曲線(xiàn)位于一、三象限，橫、縱坐標“同號”，y隨著(zhù)x的增大而減小;

②當k<0時(shí)：雙曲線(xiàn)位于二、四象限，橫、縱坐標“異號”，y隨著(zhù)x的增大而增大。

3、反比例函數圖像的對稱(chēng)性

①是軸對稱(chēng)圖形k>0時(shí)，圖像關(guān)于直線(xiàn)y=x對稱(chēng);k<0時(shí)，圖像關(guān)于y=-x對稱(chēng);

②是中心對稱(chēng)圖形關(guān)于原點(diǎn)對稱(chēng)。

4、比例系數k的幾何意義

①過(guò)雙曲線(xiàn)上任意一點(diǎn)分別向x軸和y軸作垂線(xiàn)?所得所有矩形的面積都等于|k|;

②過(guò)雙曲線(xiàn)上任意一點(diǎn)向x軸或y軸作垂線(xiàn)?由該點(diǎn)、垂足、原點(diǎn)所構成的三角形的面積都等于|k|/2。

接下來(lái)我們來(lái)看一次函數及反比例函數在中考中是怎樣考查的?這對期末考試也有幫助，因為你的老師很可能就在中考真題中扒拉一些好題出卷~

考點(diǎn)梳理

1.確定反比例函數的關(guān)系式

例題

解析

思路點(diǎn)撥

這種題型最常用的方法就是根據函數圖像，根據已知條件求解。

確定反比例函數的題型主要有三種：

(1)直接根據題意列出關(guān)系式;

(2)根據待定系數法，利用給出的一組自變量與函數的對應值求出關(guān)系式;

(3)根據待定系數法，利用函數圖象上一個(gè)點(diǎn)的坐標求出關(guān)系式。

2.反比例函數圖象及性質(zhì)的應用

例題

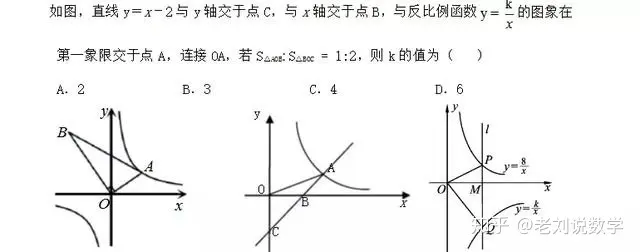
解析

思路點(diǎn)撥

利用函數和函數圖象比較數的大小，主要有三種方法：

(1)直接把x值代入函數關(guān)系式，求出相應的y值，比較數的大小;

(2)在函數圖象上描出各點(diǎn)，再根據各點(diǎn)的位置情況，比較數的大小;

(3)利用函數的增減性，比較數的大小。

3.利用反比例函數解決實(shí)際問(wèn)題

例題

解析

思路點(diǎn)撥

利用反比例函數解決生活中的實(shí)際問(wèn)題，關(guān)鍵是從實(shí)際問(wèn)題中抽象出函數關(guān)系，將文字轉化為數學(xué)語(yǔ)言。通過(guò)列函數關(guān)系式，利用反比例函數的性質(zhì)和有關(guān)的數學(xué)思想方法去解決實(shí)際問(wèn)題。要學(xué)會(huì )將數學(xué)知識應用到實(shí)際生活的各個(gè)領(lǐng)域中去。

4.綜合考查一次函數與反比例函數

例題

解析

　　 歡迎使用手機、平板等移動(dòng)設備訪(fǎng)問(wèn)中考網(wǎng)，2024中考一路陪伴同行！>>點(diǎn)擊查看