ĪĪĪĪęčų¬Ż║╚ńŽ┬łD�����Ż¼A�ĪóBā╔³c(di©Żn)╩Ūų▒ŠĆ(xi©żn)l═¼┼įĄ─ā╔éĆ(g©©)Č©³c(di©Żn)
ĪĪĪĪå¢(w©©n)Ņ}Ż║į┌ų▒ŠĆ(xi©żn)l╔ŽŪ¾ę╗³c(di©Żn)P���Ż¼╩╣Ą├PA+PBĄ─ųĄūŅą�����ĪŻ«
ĪĪĪĪĘų╬÷Ż║ū„³c(di©Żn)AĻP(gu©Īn)ė┌ų▒ŠĆ(xi©żn)lĄ─ī”ĘQ(ch©źng)³c(di©Żn)A’���Ż¼▀BĮYA’B�Ż¼Į╗ų▒ŠĆ(xi©żn)ė┌³c(di©Żn)P�����Ż¼┤╦Ģr(sh©¬)PA+PB=A’BūŅą�ĪŻ«ūC├„▀^(gu©░)│╠║▄║å(ji©Żn)å╬���Ż¼į┌ų▒ŠĆ(xi©żn)╔Žį┘╚╬╚Īę╗³c(di©Żn)P’��Ż¼P’A=P’A’����Ż¼P’A+P’B=P’A’+P’BŻŠA’B����Ż¼╦∙ęį³c(di©Żn)P╩Ū╦∙Ū¾Ż«
ĪĪĪĪ─Żą═æ¬ė├Ż║
ĪĪĪ�ĪŻ©1Ż®╚ńłD�����Ż¼š²ĘĮą╬ABCD▀ģķL(ch©óng)×ķ2���Ż¼³c(di©Żn)E╩Ū▀ģABųą³c(di©Żn)����Ż¼³c(di©Żn)P╩Ūī”ĮŪŠĆ(xi©żn)AC╔Žę╗³c(di©Żn)Ż«ätPE+PBĄ─ūŅąĪųĄ╩Ū Ż«
ĪĪĪ���ĪŻ©2Ż®╚ńłD����Ż¼ĪčOĄ─░ļÅĮ×ķ2�Ż¼³c(di©Żn)A�ĪóB�����ĪóCį┌ĪčO╔Ž���Ż¼OA⊥OB����Ż¼∠AOC=60°�����Ż¼P╩ŪOB╔Žę╗³c(di©Żn)�����Ż¼ätPA+PCĄ─ūŅąĪųĄ╩Ū Ż«
ĪĪĪ��ĪŻ©3Ż®╚ńłD��Ż¼ų▒ŠĆ(xi©żn)AB┼cx▌SĮ╗ė┌³c(di©Żn)AŻ©2�����Ż¼0Ż®�����Ż¼┼cy▌SĮ╗ė┌³c(di©Żn)BŻ©0,4Ż®��Ż¼³c(di©Żn)C��ĪóDĘųäe╩ŪOA��ĪóABĄ─ųą³c(di©Żn)��Ż¼P╩ŪOB╔Žę╗³c(di©Żn)����Ż¼Ū¾Ī„PCDų▄ķL(ch©óng)Ą─ūŅąĪųĄŻ«
ĪĪĪĪęį╔ŽÄūŅ}╩Ū─Żą═1į┌▓╗═¼Ņ}ą═ųąĄ─▀\ė├�����Ż¼═¼īW(xu©”)éā╚ń╣¹─▄ŠÜ│╔“╗č█ĮŠ””�����Ż¼╔Ųė┌į┌ūā╗»Ą─Śl╝■ųąšęĄĮ▓╗ūāĄ─öĄīW(xu©”)─Żą═��Ż¼“ęį▓╗ūāæ¬╚f(w©żn)ūā”����Ż¼Š═┐╔ęįŽ±īO╬“┐šę╗śė│╔×ķ┐╝ł÷(ch©Żng)╔ŽĄ─“ČĘæä┘Ę”Ż«╚ń╣¹░č─Żą═1ųąĄ─Śl╝■╔įū„š{š¹�Ż¼ėų┐╔ęįĄ├ĄĮ╦³Ą─ę╗ą®═ŲÅV─Żą═Ż«
ĪĪĪĪ┤░ĖŻ║
ĪĪĪĪ═ŲÅV1Ż║
ĪĪĪĪęčų¬Ż║╚ńłD��Ż¼³c(di©Żn)P╩Ū∠AOBā╚ę╗Č©³c(di©Żn)Ż«
ĪĪĪĪå¢(w©©n)Ņ}Ż║Ęųäeį┌OA���ĪóOB▀ģ╔Žšę³c(di©Żn)M��ĪóN��Ż¼╩╣Ī„PMNĄ─ų▄ķL(ch©óng)ūŅą�����ĪŻ«
ĪĪĪĪĘų╬÷Ż║Ī„PMNĄ─ų▄ķL(ch©óng)=PM+MN+NP�����Ż¼┐╔ęį└¹ė├ū„▌Sī”ĘQ(ch©źng)�����Ż¼░č▀@╚²ŚlŠĆ(xi©żn)Č╬▐D╗»×ķ═¼ę╗ų▒ŠĆ(xi©żn)╔ŽĄ─ŠĆ(xi©żn)Č╬Ż«╚ńłD����Ż¼Ęųäeū„³c(di©Żn)PĻP(gu©Īn)ė┌OA��ĪóOBĄ─ī”ĘQ(ch©źng)³c(di©Żn)P’����ĪóP’’�Ż¼▀BĮYP’P’’�Ż¼ĘųäeĮ╗OA��ĪóOBė┌³c(di©Żn)M��ĪóN�Ż¼▀BĮYPM���ĪóPN���Ż¼┤╦Ģr(sh©¬)PM=P’M�����Ż¼PN=P’N���Ż¼Ī„PMNĄ─ų▄ķL(ch©óng)=PM+MN+NP=P’P’’�Ż¼┤╦Ģr(sh©¬)ų▄ķL(ch©óng)ūŅą���ĪŻ«
ĪĪĪĪ─Żą═æ¬ė├Ż║╚ńłD�����Ż¼³c(di©Żn)CŻ©1,0Ż®��Ż¼ų▒ŠĆ(xi©żn)y=-x+7┼cā╔ū°ś╦▌SĘųäeĮ╗ė┌A(y©¬ng)��ĪóBā╔³c(di©Żn)�����Ż¼D����ĪóEĘųäe╩ŪAB�����ĪóOA╔ŽĄ─äė(d©░ng)³c(di©Żn)���Ż¼ätĪ„CDEų▄ķL(ch©óng)Ą─ūŅąĪųĄ╩Ū
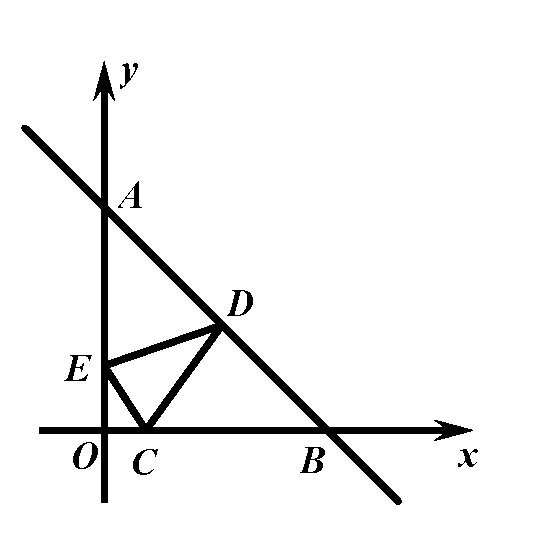
Ż«
ĪĪĪĪ┤░ĖŻ║10
ĪĪĪĪ═ŲÅV2Ż║
ĪĪĪĪęčų¬Ż║³c(di©Żn)P�����ĪóQ╩Ū∠AOBā╚▓┐?j©¼)╔Č©³c(di©Żn)Ż«
ĪĪĪĪå¢(w©©n)Ņ}Ż║Ęųäeį┌ų▒ŠĆ(xi©żn)OA��ĪóOB╔Žšę³c(di©Żn)M����ĪóN��Ż¼╩╣╦─▀ģą╬PMNQĄ─ų▄ķL(ch©óng)ūŅą�����ĪŻ«
ĪĪĪĪĘų╬÷Ż║ę“×ķPQĄ─ķL(ch©óng)Č╚╩ŪČ©ųĄ����Ż¼ę¬╩╣╦─▀ģą╬PMNQĄ─ų▄ķL(ch©óng)ūŅąĪ���Ż¼Š═╩Ūę¬╩╣PM+MN+NQĄ─ųĄūŅą�����ĪŻ«ū„³c(di©Żn)PĻP(gu©Īn)ė┌OAĄ─ī”ĘQ(ch©źng)³c(di©Żn)P’���Ż¼ū„³c(di©Żn)QĻP(gu©Īn)ė┌OBĄ─ī”ĘQ(ch©źng)³c(di©Żn)Q’����Ż¼▀BĮYP’Q’��Ż¼ĘųäeĮ╗ų▒ŠĆ(xi©żn)OA����ĪóOBė┌³c(di©Żn)M��ĪóN�Ż¼▀BĮYPM���ĪóMN��ĪóNQ��Ż¼ę“×ķPM=P’M�����Ż¼QN=Q’N�����Ż¼╦∙ęį╦─▀ģą╬PMNQĄ─ų▄ķL(ch©óng)=PM+MN+NQ+QP=P’Q’+PQ����Ż¼ę“×ķPQ╩ŪČ©ųĄ���Ż¼Č°PM+MN+NQĄ─ūŅąĪųĄ×ķP’Q’Ą─ķL(ch©óng)Č╚�����Ż¼╦∙ęį┤╦Ģr(sh©¬)╦─▀ģą╬PMNQĄ─ų▄ķL(ch©óng)ūŅą�ĪŻ«
ĪĪĪĪ─Żą═æ¬ė├Ż║į┌ŲĮ├µų▒ĮŪū°ś╦ŽĄųą�����Ż¼³c(di©Żn)AŻ©-8,3Ż®�����Ż¼³c(di©Żn)BŻ©-4,5Ż®�Ż¼³c(di©Żn)CŻ©0�Ż¼nŻ®���Ż¼³c(di©Żn)DŻ©m��Ż¼0Ż®�����Ż¼«ö╦─▀ģą╬ABCDų▄ķL(ch©óng)ūŅČ╠Ģr(sh©¬)���Ż¼Ū¾mŻ║nĄ─ųĄŻ«
ĪĪĪĪ┤░ĖŻ║
ĪĪĪĪį┌ūā╗»╚f(w©żn)Ū¦Ą─ęčų¬Śl╝■Ž┬�Ż¼─▄ē“šęĄĮ▓╗ūāĄ─ęÄ┬╔�����Ż¼▀@┼cĪČęūĮø(j©®ng)ĪĘųąĻU╩÷Ą─“ūā┼c▓╗ūā”Ą─ųŪ╗█ŽÓ╬Ū║ŽŻ«╚╦ŅÉ(l©©i)ūŅĖ▀Ą─ųŪ╗█��Ż¼Š═╩Ū“ęį▓╗ūāæ¬╚f(w©żn)ūā”��Ż¼▀@ę▓╩ŪöĄīW(xu©”)īW(xu©”)┴ĢĄ─¤o(w©▓)ö│Ę©īÜŻ«
ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC����ĪóŲĮ░ÕĄ╚ęŲäė(d©░ng)įOéõįL(f©Żng)å¢(w©©n)ųą┐╝ŠW(w©Żng)���Ż¼2023ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą����ŻĪ>>³c(di©Żn)ō¶▓ķ┐┤






